算数が苦手なお子さんで以下のようなことでお困りの方は、本記事を読んで、丸暗記するように仕向けてみてください。
- テストで時間が足りない
- 計算ミスが多い
この数字を丸暗記することで、大幅に改善すると思います。
毎日、ご飯前に暗唱する、トイレに一覧を貼って読むなどで、目にする習慣づけして身に着けることをお勧めします。
中学受験の算数で覚えておくべき数字(3選+2)
算数で、頻出の数字3選です。
騙されたと思って丸暗記しておいて、絶対損はしません。
3選は、必ず覚えてください。
おまけで2つ紹介します。覚えておくと使えることがあると思います。
円周率 の倍数
3.14を使った問題は、図形問題だけでなく、計算問題でも出題されることが多いです。
例えば、
3.14 × 3 – 31.4 + 28.26
みたいな問題が出たときに、「28.26」が「3.14 × 9 」ということが思いつけば、分配法則を使うことで、「3.14 × ( 3 – 10 + 9 )」という式になるため、少数を含む計算が1度だけで済みます。
しかも、「 3.14 × 2 = 6.28」を暗記していれば、計算するのは分配法則の()内の中だけなので、格段に計算ミスする確率が下がるはずです。
計算ミスが減るだけでなく、計算速度も格段に速くなるので、円周率に関する暗記は必須です。
以下の内容を表にして、丸暗記してください。
- 3.14 × 2 = 6.2
- 3.14 × 3 = 9.42
- 3.14 × 4 = 12.56
- 3.14 × 5 = 15.7
- 3.14 × 6 = 18.84
- 3.14 × 7 = 21.98
- 3.14 × 8 = 25.12
- 3.14 × 9 = 28.26
1/8の倍数の分数⇔少数変換
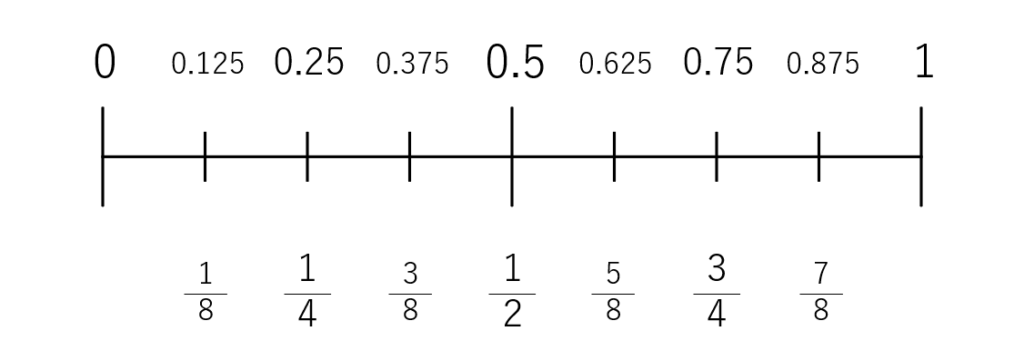
「1/8 = 0.125」の倍数を丸暗記しておくことをお勧めします。
0.375、0.525、0.875のあたりは覚えづらいですが、これを簡単に変換できるようになると計算速度で差がつきます。
図解して覚えておくと、イメージつきやすいかもしれません。
平方数
図形問題や、数の法則の問題などで、使用する頻度が多い数です。
図形問題では計算ミスが減ります。
数の法則では、法則を見つける(ひらめく)のに絶大な効果があります。
1~20ぐらいまでは、暗唱できるようにしておくと便利です。

おまけ 2つ
上記3つほど重要ではありませんが、覚えておいて損はない数字です。
余力があったら覚えておくと役に立つことがあると思います。
素数
規則性の問題や、計算問題で素数を覚えていると、ひらめきやすい問題が多々あります。
素数とは: 1より大きい自然数で、正の約数が 1 と自分自身のみであるもののこと(Wikipediaより)
2、3、5、7、11、13、17、19、23、29、31、37、41、43、53、59、61、71、73、79、83、89、97
1は素数ではないことに注意してください。
1桁、2桁の素数は言えるようになっているとよいでしょう。
三角数
規則性の問題で、使うことがよくあります。覚えておくと便利です。
三角数とは:正三角形の形に点を並べたときにそこに並ぶ点の総数のこと
(Wikipediaより一部抜粋)
この数字を見たときに、何段目まで足した数と「パッ」と思いつくぐらいになると、問題を解くスピードが速くなります。
三角数をイメージするときに、以下の図をイメージすると分かりやすいのではないかと思います。
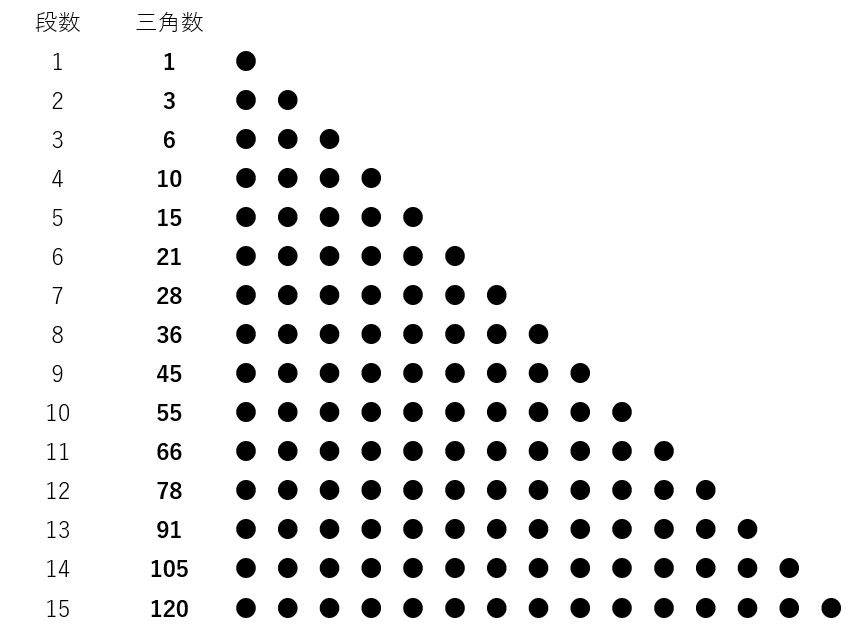
1段増えると、1つ増えていますよね。
n段目の場合は、1からnまでの総和 [ (1+n)× n ÷ 2 ] となります。



コメント