中学受験算数では、長文問題が増えてきています(算数なのに長文)。
文章を読みながら、出てくる数字とその文面を的確にとらえることが必要になります。
倍数、約数の考え方や、コツを覚えておくと、出てくる数字に関連する数字のヒラメキや、推測がしやすくなり、問題を解くスピードが上がると思います!
この記事では、約数、倍数の基本と覚えておくべきコツを紹介します。
倍数と約数について
大きな数が出てきた時、その数が何の倍数なのか、その数の約数がいくつあるのか、ということが分かって当然という問題も、当たり前のように出てきます。
倍数、約数の定義と、倍数の見分け方などを紹介します。
倍数
ある数を何倍かしてできた数のことを倍数といいます。
※1倍も含むことに注意してください。
公倍数
- 2個以上の数に共通な倍数のことを公倍数といいます。
- 公倍数の中の、値が最も小さいものを最小公倍数といいます。
- 公倍数は全て、最小公倍数の倍数となる。
倍数の性質(※超重要なコツ)
倍数の性質として、以下の7つは絶対に丸暗記することをお勧めします。
- ■の倍数+■の倍数(■の倍数ー■の倍数)=■の倍数
- 2の倍数 :1の位が偶数(0、2、4、6、8)。
- 3の倍数 :すべての位の数の和が3の倍数。
- 4の倍数 :下2ケタが4の倍数、または00。
- 5の倍数 :1の位が0、または5。
- 6の倍数 :2の倍数の性質と、3の倍数の性質の両方を持つ。
- 9の倍数 :すべての位の数の和が9の倍数。
上記の記載だけでは、理解しづらいと思うので、例をいくつか紹介します。
大きな数を適当に作って、その数が何の倍数になるか、考えてみる遊びをしてみると覚えやすいかもしれませんね!!
【例1】3の倍数について
219の場合。
2+1+9=12で、12は3の倍数(3×4)なので、「219」は3の倍数であることがわかる。
【例2】4の倍数
(その1)736の場合。
下2ケタの「36」が4の倍数(4×9)なので、「736」は4の倍数であることがわかる。
(その2)3500の場合。
下2ケタが「00」なので、100の倍数(4×25)の倍数であることから、4の倍数であることがわかる。
【例3】6の倍数
456の場合。
1の位が「6」で偶数なので、2の倍数の性質を持ちます。
全ての位の和が、4+5+6=15で、「15」は3の倍数(3×5)なので、3の倍数の性質も持ちます。
したがって、「456」は6の倍数であることがわかります。
【例4】9の倍数
51327の場合。
全ての位の和が、5+1+3+2+7=18で、「18」は9の倍数(9×2)なので、「51327」は9の倍数であることがわかります。
約数
ある数を割ったときに、わり切れる数のこと。
公約数
- 2個以上の数に共通する約数のことを公約数といいます。
- 公約数は全て、最大公約数の約数です。
■×△=★ の時、★は、■の倍数であり、△の倍数です。
また■も、△も★の約数となります。
倍数、約数を使うこと文章題
以下のような文章題が出たときに、どんな式のことを問われているのかピンとこないお子さんが多いようです。
【例1】ある整数を18でわったところ、商が6で、あまりが13となりました。ある整数を求めなさい。
【例2】6でわると3あまり、7でわると4あまる、2ケタで最も大きい整数を求めなさい。
最初は、文章題から、どんな式(割り算)を使うのかをイメージできません。
文章と式がちゃんと紐づくようになるとスムーズに解けるようになります。
以下の内容を覚えると、文章題でもスッキリ解ける問題が増えるとおもいます。
割り算の商とあまり。わる数とわられる数。
割り算は以下の式で表現できます。
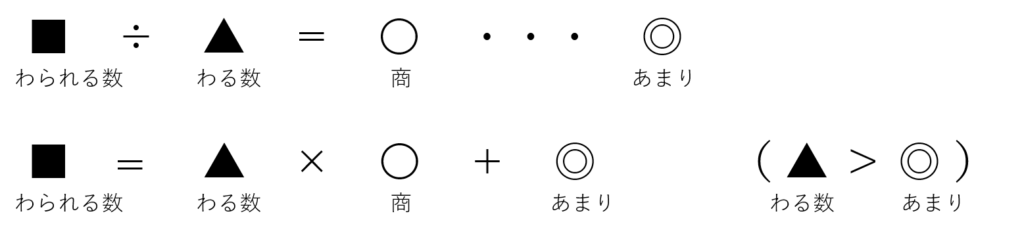
■を▲でわる
「■を▲でわる」は、式で書くと、「■ ÷ ▲」のことである。
この文章の内容を、計算式に変換できるように覚えておいてください。
▲でわって◎あまる数
ある数を7でわって、3あまる場合、「■ ÷ 7 = ○ ・・・3」となります。
言い換えると、「■ = 7 × ○ + 3」となります。
したがって、■は「7の倍数に3を足した数」となります。
「▲でわって◎あまる数」とは、「▲の倍数に◎を足した数」=「▲の倍数+◎」
と言い換えることができます。
また、「▲の倍数から(▲ ー ◎)を引いた数」=「▲の倍数ー(▲ー◎)」とも言い換えることができることを覚えておいてください。
ちょっと分かりづらいですよね。
例で説明します。
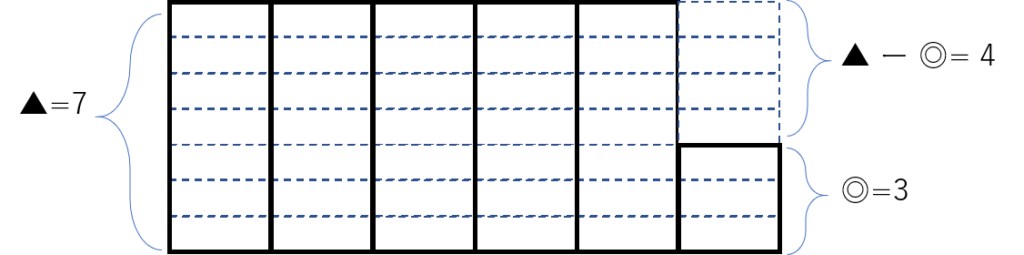
【例】■=38、○=5、▲=7、◎=3を例にして図解します。
38 = 7 × 5 + 3 となりますが、
38 = 7 × 6 – ( 7 – 3) とも考えることができます。
の考え方を使って、先の例題【例2】を解くことができます。
【例2】6でわると3あまり、7でわると4あまる、2ケタで最も大きい整数を求めなさい。
[解説]
6でわると3あまる数 = 6の倍数+3 または 6の倍数ー3
7でわると4あまる数 = 7の倍数+4 または 7の倍数ー3
となり、2つの条件をどちらも満たす数は、「6の倍数ー3」でもあり「7の公倍数ー3」であることから、「6と7の公倍数ー3 」となります。
「6と7の公倍数」=42 なので、「42の倍数ー3」で2ケタの中で最も多い整数が答えとなります。
42×1-3=39
42×2-3=81
42×3-3=123 ← 3ケタなのでNG
以上のことから、答えは「81」となります。
(参考)問題例
長方形のタイルを使って正方形を作る
【問】タテ:4、ヨコ:5の長方形のタイルを使って、もっとも小さい正方形を作るのに、何枚のタイルが必要になるか求めなさい。
[解説]
公倍数を使って考えます。
4と5の最小公倍数「20」が、最も小さい正方形の1辺の長さとなる。

したがって、タテ、ヨコの枚数はそれぞれ
タテ:20 ÷ 4 = 5(枚)
ヨコ:20 ÷ 5 = 4(枚)
となり、合計は 5 × 4 = 20(枚)が求める答えとなります。
長方形の紙を正方形に切り分ける
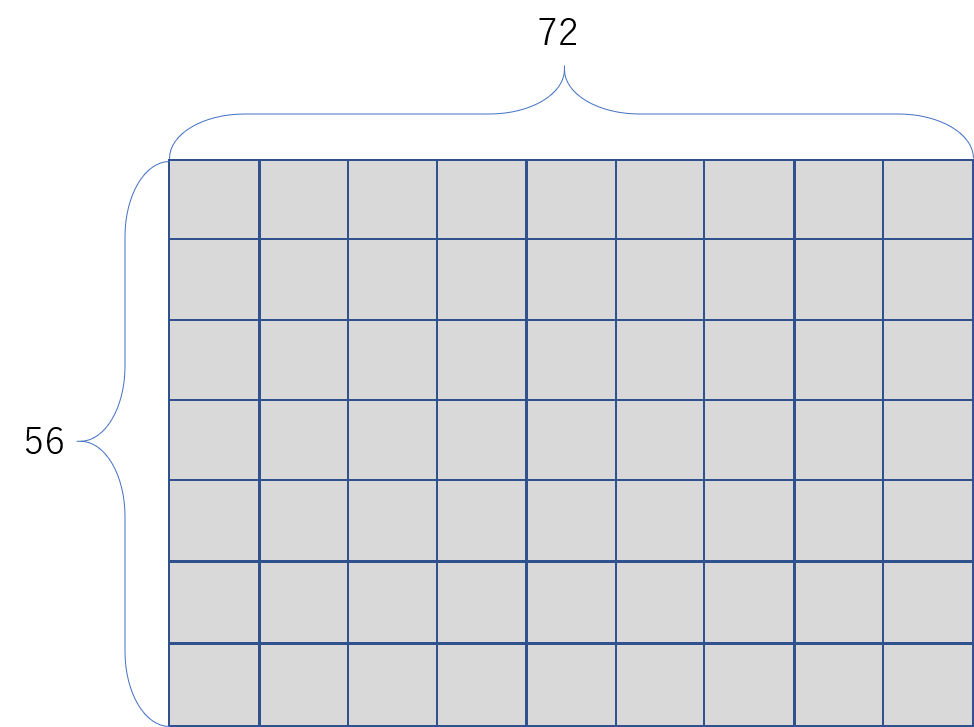
【問】タテ:56、ヨコ:72の長さの長方形を、正方形の形で切り分ける場合、もっとも大きな正方形の1辺の長さを求めなさい。
[解説]
正方形にするために、タテとヨコを同じ長さで切り分けます。
タテとヨコを同じ数でわって、あまりが出ないようにするためには、公約数を使います。
もっとも大きな正方形を作るためには、最大公約数を求めればよいのです。
56と72の公約数は、、、
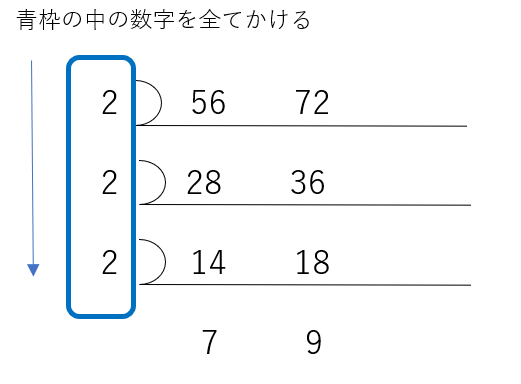
2 × 2 × 2 = 8 となるので、答えは「8」です。
まとめ
倍数、約数のコツや考え方を覚えておくことで、算数の文章題や計算問題でヒラメキや推測が立てやすくなり、問題が解きやすくなります。
是非覚えておいてください。
良い文章題の例が思いついたら、記事の追記してみます。
今日は、ここまで。
それでは、また。


コメント